A83484.Cyclic Components

给定一张 $n$ 个点，$m$ 条边的无向图。保证无重边、无自环。在该图的所有连通块中，你需要找出环的个数。

无向图的环的定义如下：

原无向图中的一个子图被定义为环，当且仅当它的点集重新排序后可以满足如下条件：

• 第一个点与第二个点通过一条边相连接；
• 第二个点与第三个点通过一条边相连接；
• ……
• 最后一个点与第一个点通过一条边相连接。
• 所有的边都应当是不同的。
• 其边集不应当包含除了以上所述的边以外的任何边。

这样，我们就称这个子图（点 + 边）为环。

根据定义，一个环至少需要包含三个点，且边数与点数应当是相同的。

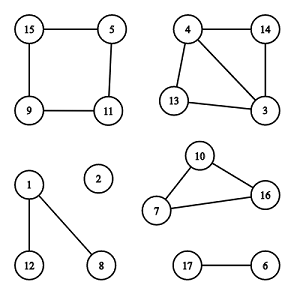
例如对于上图，共有 $6$ 个联通块，但只有 $[7,10,16]$ 和 $[5,11,9,15]$ 这两个联通块是环。

第一行两个整数 $n$ 和 $m$ $(1 \le n \le 2 \cdot 10^5, 0 \le m \le 2 \cdot 10^5)$，分别表示图的点数和无向边数。

接下来 $m$ 行，第 $i$ 行包含两个整数 $v_i, u_i$ $(1 \le v_i, u_i \le n, u_i \not = v_i)$，表示第 $i$ 条边连接着 $v_i$ 与 $u_i$ 两点。

输出一行一个整数，表示环的个数。

样例说明
在第一个样例中，只有 $[3, 4, 5]$ 这个联通块是一个环。

第二个样例就对应着题目解释中的图片。