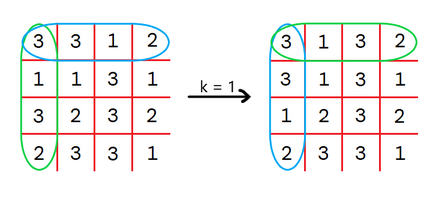
CF1713E.Cross Swapping

You are given a square matrix $A$ of size $n \times n$ whose elements are integers. We will denote the element on the intersection of the $i$ -th row and the $j$ -th column as $A_{i,j}$ .

You can perform operations on the matrix. In each operation, you can choose an integer $k$ , then for each index $i$ ( $1 \leq i \leq n$ ), swap $A_{i, k}$ with $A_{k, i}$ . Note that cell $A_{k, k}$ remains unchanged.

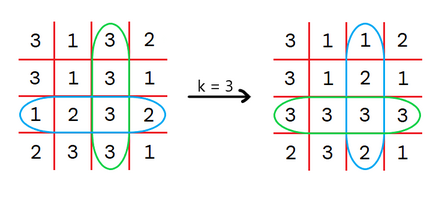
For example, for $n = 4$ and $k = 3$ , this matrix will be transformed like this:

The operation $k = 3$ swaps the blue row with the green column.You can perform this operation any number of times. Find the lexicographically smallest matrix $^\dagger$ you can obtain after performing arbitrary number of operations.

${}^\dagger$ For two matrices $A$ and $B$ of size $n \times n$ , let $a_{(i-1) \cdot n + j} = A_{i,j}$ and $b_{(i-1) \cdot n + j} = B_{i,j}$ . Then, the matrix $A$ is lexicographically smaller than the matrix $B$ when there exists an index $i$ ( $1 \leq i \leq n^2$ ) such that $a_i < b_i$ and for all indices $j$ such that $1 \leq j < i$ , $a_j = b_j$ .

The first line contains a single integer $t$ ( $1 \leq t \leq 10^5$ ) — the number of test cases.

The first line of each test case contains a single integer $n$ ( $1 \leq n \leq 1000$ ) — the size of the matrix.

The $i$ -th line of the next $n$ lines contains $n$ integers $A_{i, 1}, A_{i, 2}, \dots, A_{i, n}$ ( $1 \le A_{i, j} \le 10^9$ ) — description of the matrix $A$ .

It is guaranteed that the sum of $n^2$ over all test cases does not exceed $10^6$ .

For each test case, print $n$ lines with $n$ integers each — the lexicographically smallest matrix.

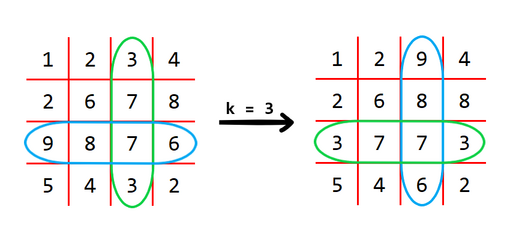
Note that in every picture below the matrix is transformed in such a way that the blue rows are swapped with the green columns.

In the first test case, we can perform $1$ operation for $k = 3$ . The matrix will be transformed as below:

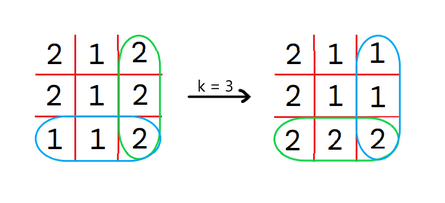In the second test case, we can perform $2$ operations for $k = 1$ and $k = 3$ :