CF1725C.Circular Mirror

Pak Chanek has a mirror in the shape of a circle. There are $N$ lamps on the circumference numbered from $1$ to $N$ in clockwise order. The length of the arc from lamp $i$ to lamp $i+1$ is $D_i$ for $1 \leq i \leq N-1$ . Meanwhile, the length of the arc between lamp $N$ and lamp $1$ is $D_N$ .

Pak Chanek wants to colour the lamps with $M$ different colours. Each lamp can be coloured with one of the $M$ colours. However, there cannot be three different lamps such that the colours of the three lamps are the same and the triangle made by considering the three lamps as vertices is a right triangle (triangle with one of its angles being exactly $90$ degrees).

The following are examples of lamp colouring configurations on the circular mirror.

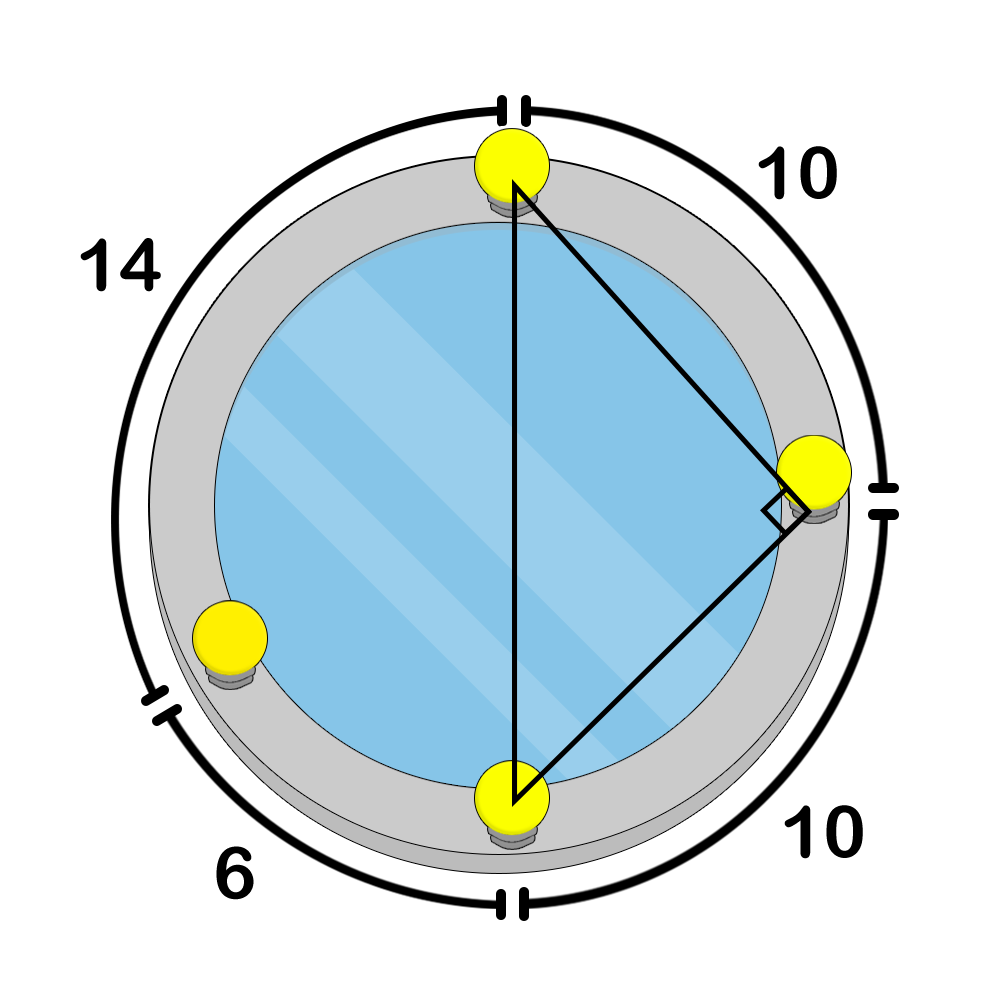
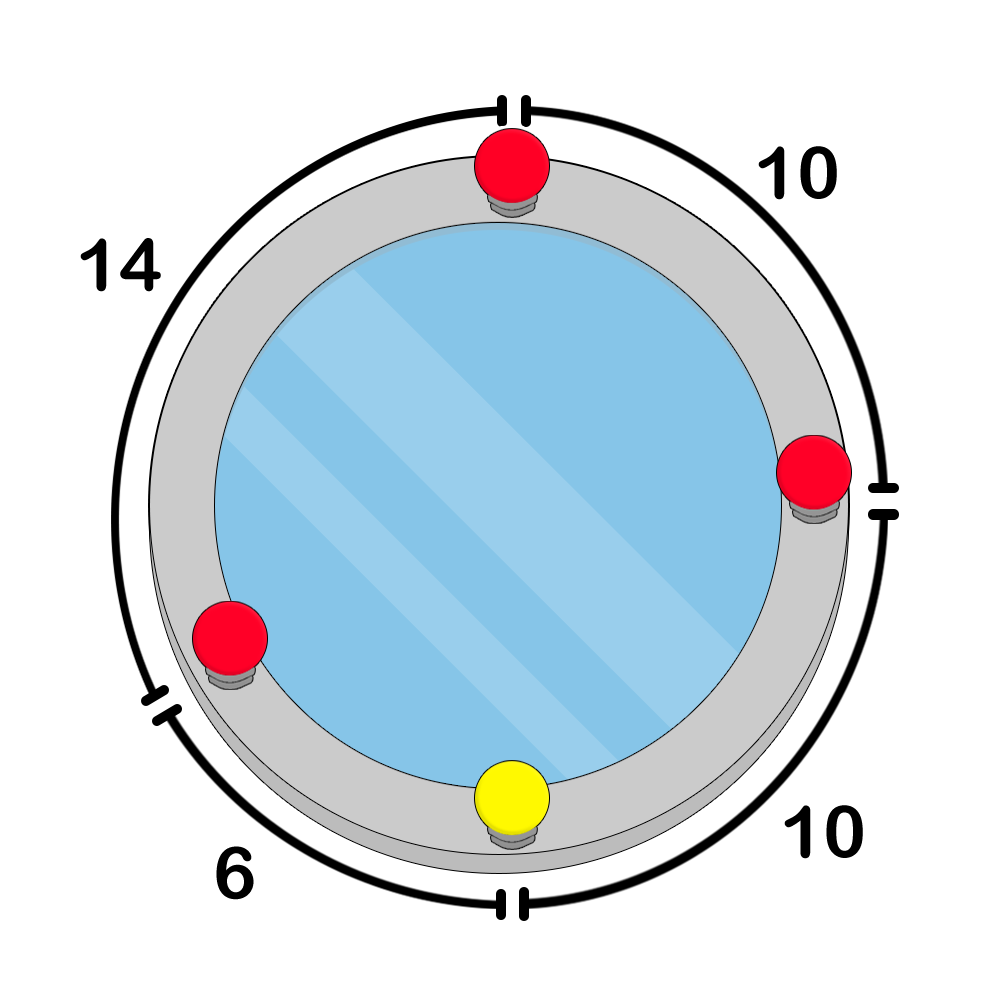
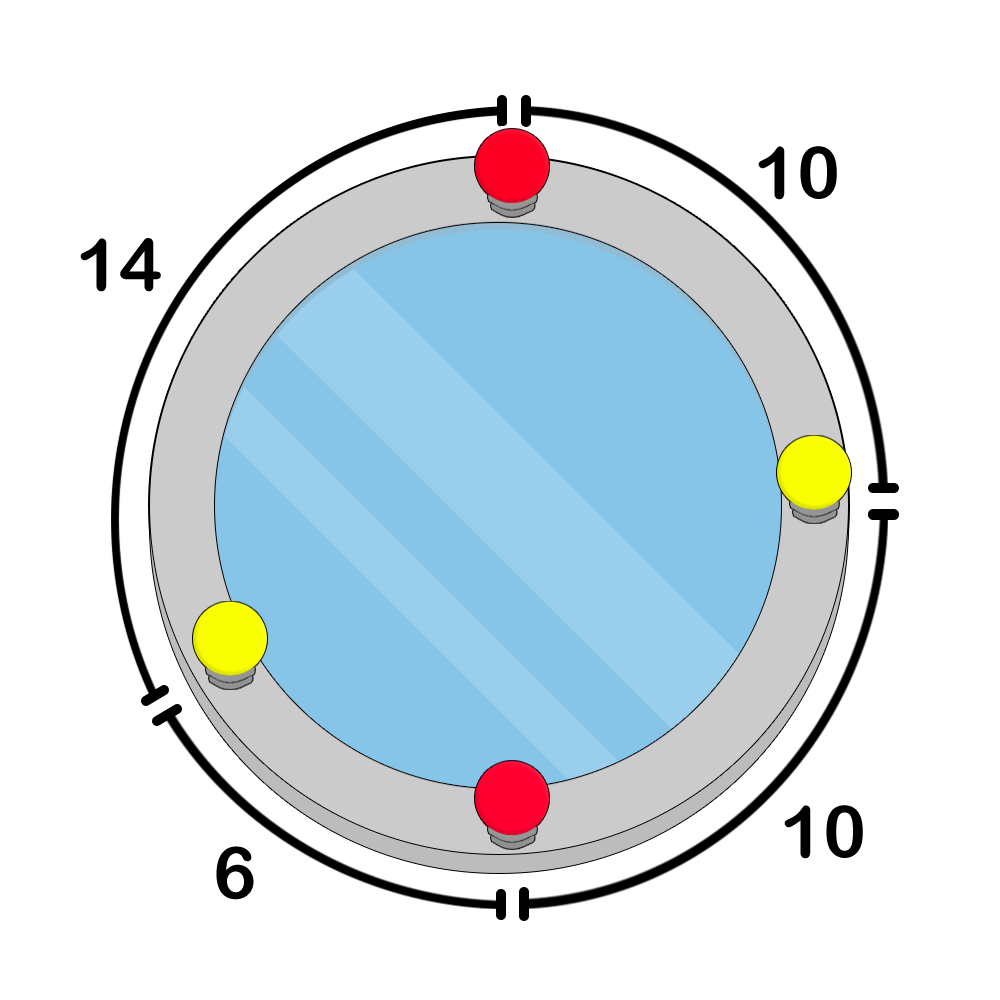Figure 1. an example of an incorrect colouring because lamps $1$ , $2$ , and $3$ form a right triangleFigure 2. an example of a correct colouringFigure 3. an example of a correct colouringBefore colouring the lamps, Pak Chanek wants to know the number of distinct colouring configurations he can make. Count the number of distinct possible lamp colouring configurations, modulo $998\,244\,353$ .

The first line contains two integers $N$ and $M$ ( $1 \le N \le 3 \cdot 10^5$ , $2 \le M \le 3 \cdot 10^5$ ) — the number of lamps in the mirror and the number of different colours used.

The second line contains $N$ integers $D_1, D_2, \ldots, D_N$ ( $1 \le D_i \le 10^9$ ) — the lengths of the arcs between the lamps in the mirror.

An integer representing the number of possible lamp colouring configurations, modulo $998\,244\,353$ .

In the first example, all correct lamp colouring configurations are $[1, 1, 2, 1]$ , $[1, 1, 2, 2]$ , $[1, 2, 1, 2]$ , $[1, 2, 2, 1]$ , $[1, 2, 2, 2]$ , $[2, 1, 1, 1]$ , $[2, 1, 1, 2]$ , $[2, 1, 2, 1]$ , $[2, 2, 1, 1]$ , and $[2, 2, 1, 2]$ .