CF1506F.Triangular Paths

Consider an infinite triangle made up of layers. Let's number the layers, starting from one, from the top of the triangle (from top to bottom). The $k$ -th layer of the triangle contains $k$ points, numbered from left to right. Each point of an infinite triangle is described by a pair of numbers $(r, c)$ ( $1 \le c \le r$ ), where $r$ is the number of the layer, and $c$ is the number of the point in the layer. From each point $(r, c)$ there are two directed edges to the points $(r+1, c)$ and $(r+1, c+1)$ , but only one of the edges is activated. If $r + c$ is even, then the edge to the point $(r+1, c)$ is activated, otherwise the edge to the point $(r+1, c+1)$ is activated. Look at the picture for a better understanding.

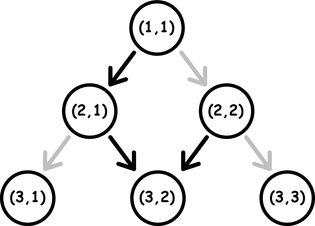Activated edges are colored in black. Non-activated edges are colored in gray.From the point $(r_1, c_1)$ it is possible to reach the point $(r_2, c_2)$ , if there is a path between them only from activated edges. For example, in the picture above, there is a path from $(1, 1)$ to $(3, 2)$ , but there is no path from $(2, 1)$ to $(1, 1)$ .

Initially, you are at the point $(1, 1)$ . For each turn, you can:

• Replace activated edge for point $(r, c)$ . That is if the edge to the point $(r+1, c)$ is activated, then instead of it, the edge to the point $(r+1, c+1)$ becomes activated, otherwise if the edge to the point $(r+1, c+1)$ , then instead if it, the edge to the point $(r+1, c)$ becomes activated. This action increases the cost of the path by $1$ ;
• Move from the current point to another by following the activated edge. This action does not increase the cost of the path.

You are given a sequence of $n$ points of an infinite triangle $(r_1, c_1), (r_2, c_2), \ldots, (r_n, c_n)$ . Find the minimum cost path from $(1, 1)$ , passing through all $n$ points in arbitrary order.

The first line contains one integer $t$ ( $1 \le t \le 10^4$ ) is the number of test cases. Then $t$ test cases follow.

Each test case begins with a line containing one integer $n$ ( $1 \le n \le 2 \cdot 10^5$ ) is the number of points to visit.

The second line contains $n$ numbers $r_1, r_2, \ldots, r_n$ ( $1 \le r_i \le 10^9$ ), where $r_i$ is the number of the layer in which $i$ -th point is located.

The third line contains $n$ numbers $c_1, c_2, \ldots, c_n$ ( $1 \le c_i \le r_i$ ), where $c_i$ is the number of the $i$ -th point in the $r_i$ layer.

It is guaranteed that all $n$ points are distinct.

It is guaranteed that there is always at least one way to traverse all $n$ points.

It is guaranteed that the sum of $n$ over all test cases does not exceed $2 \cdot 10^5$ .

For each test case, output the minimum cost of a path passing through all points in the corresponding test case.