CF1508C.Complete the MST
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
As a teacher, Riko Hakozaki often needs to help her students with problems from various subjects. Today, she is asked a programming task which goes as follows.
You are given an undirected complete graph with n nodes, where some edges are pre-assigned with a positive weight while the rest aren't. You need to assign all unassigned edges with non-negative weights so that in the resulting fully-assigned complete graph the XOR sum of all weights would be equal to 0 .
Define the ugliness of a fully-assigned complete graph the weight of its minimum spanning tree, where the weight of a spanning tree equals the sum of weights of its edges. You need to assign the weights so that the ugliness of the resulting graph is as small as possible.
As a reminder, an undirected complete graph with n nodes contains all edges (u,v) with 1≤u<v≤n ; such a graph has 2n(n−1) edges.
She is not sure how to solve this problem, so she asks you to solve it for her.
输入格式
The first line contains two integers n and m ( 2≤n≤2⋅105 , 0≤m≤min(2⋅105,2n(n−1)−1) ) — the number of nodes and the number of pre-assigned edges. The inputs are given so that there is at least one unassigned edge.
The i -th of the following m lines contains three integers ui , vi , and wi ( 1≤ui,vi≤n , u=v , 1≤wi<230 ), representing the edge from ui to vi has been pre-assigned with the weight wi . No edge appears in the input more than once.
输出格式
Print on one line one integer — the minimum ugliness among all weight assignments with XOR sum equal to 0 .
输入输出样例
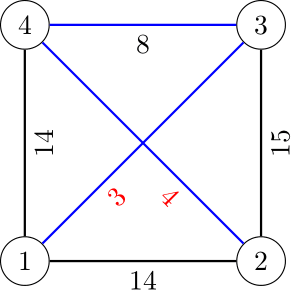
输入#1
4 4 2 1 14 1 4 14 3 2 15 4 3 8
输出#1
15
输入#2
6 6 3 6 4 2 4 1 4 5 7 3 4 10 3 5 1 5 2 15
输出#2
0
输入#3
5 6 2 3 11 5 3 7 1 4 10 2 4 14 4 3 8 2 5 6
输出#3
6
说明/提示
The following image showcases the first test case. The black weights are pre-assigned from the statement, the red weights are assigned by us, and the minimum spanning tree is denoted by the blue edges.