CF1508F.Optimal Encoding

Touko's favorite sequence of numbers is a permutation $a_1, a_2, \dots, a_n$ of $1, 2, \dots, n$, and she wants some collection of permutations that are similar to her favorite permutation.

She has a collection of $q$ intervals of the form $[l_i, r_i]$ with $1 \le l_i \le r_i \le n$. To create permutations that are similar to her favorite permutation, she coined the following definition:

• A permutation $b_1, b_2, \dots, b_n$ allows an interval $[l', r']$ to holds its shape if for any pair of integers $(x, y)$ such that $l' \le x \lt y \le r'$, we have $b_x \lt b_y$ if and only if $a_x \lt a_y$.
• A permutation $b_1, b_2, \dots, b_n$ is $k$-similar if $b$ allows all intervals $[l_i, r_i]$ for all $1 \le i \le k$ to hold their shapes.

Yuu wants to figure out all $k$-similar permutations for Touko, but it turns out this is a very hard task; instead, Yuu will encode the set of all $k$-similar permutations with directed acylic graphs (DAG). Yuu also coined the following definitions for herself:

• A permutation $b_1, b_2, \dots, b_n$ satisfies a DAG $G'$ if for all edge $u \to v$ in $G'$, we must have $b_u \lt b_v$.
• A $k$-encoding is a DAG $G_k$ on the set of vertices $1, 2, \dots, n$ such that a permutation $b_1, b_2, \dots, b_n$ satisfies $G_k$ if and only if $b$ is $k$-similar.

Since Yuu is free today, she wants to figure out the minimum number of edges among all $k$-encodings for each $k$ from $1$ to $q$.

塔子最喜欢的数字序列是 $1, 2, \dots, n$ 的一个排列 $a_1, a_2, \dots, a_n$，她希望得到一些与她最喜欢的排列“相似”的排列集合。

她拥有 $q$ 个形如 $[l_i, r_i]$ 的区间（满足 $1 \le l_i \le r_i \le n$）。为了定义与她最喜欢的排列“相似”的排列，她引入了如下概念：

• 排列 $b_1, b_2, \dots, b_n$ 允许区间 $[l', r']$ 保持其形状，当且仅当：对任意整数对 $(x, y)$ 满足 $l' \le x \lt y \le r'$，均有 $b_x \lt b_y$ 当且仅当 $a_x \lt a_y$。
• 排列 $b_1, b_2, \dots, b_n$ 是 $k$-相似的，当且仅当 $b$ 允许所有区间 $[l_i, r_i]$（其中 $1 \le i \le k$）均保持其形状。

悠希望能为塔子找出所有 $k$-相似排列，但结果发现这是一项非常困难的任务；于是悠转而用有向无环图（DAG） 来编码所有 $k$-相似排列的集合。悠还为自己定义了如下概念：

• 排列 $b_1, b_2, \dots, b_n$ 满足 DAG $G'$，当且仅当：对 $G'$ 中每一条边 $u \to v$，均有 $b_u \lt b_v$。
• 一个 $k$-编码 是定义在顶点集 $\{1, 2, \dots, n\}$ 上的一个 DAG $G_k$，使得排列 $b_1, b_2, \dots, b_n$ 满足 $G_k$ 当且仅当 $b$ 是 $k$-相似的。

由于悠今天比较空闲，她希望对每个 $k = 1, 2, \dots, q$，求出所有 $k$-编码中边数的最小值。

The first line contains two integers $n$ and $q$ ($1 \le n \le 25\,000$, $1 \le q \le 100\,000$).

The second line contains $n$ integers $a_1, a_2, \dots, a_n$ which form a permutation of $1, 2, \dots, n$.

The $i$-th of the following $q$ lines contains two integers $l_i$ and $r_i$. ($1 \le l_i \le r_i \le n$).

第一行包含两个整数 $n$ 和 $q$（$1 \le n \le 25\,000$，$1 \le q \le 100\,000$）。

第二行包含 $n$ 个整数 $a_1, a_2, \dots, a_n$，它们构成 $1, 2, \dots, n$ 的一个排列。

接下来的 $q$ 行中，第 $i$ 行包含两个整数 $l_i$ 和 $r_i$（$1 \le l_i \le r_i \le n$）。

Print $q$ lines. The $k$-th of them should contain a single integer — The minimum number of edges among all $k$-encodings.

输出 $q$ 行。其中第 $k$ 行应包含一个整数——所有 $k$-编码中边数的最小值。

For the first test case:

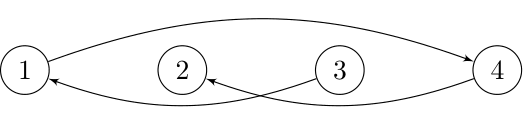
• All $1$-similar permutations must allow the interval $[1, 3]$ to hold its shape. Therefore, the set of all $1$-similar permutations is ${[3, 4, 2, 1], [3, 4, 1, 2], [2, 4, 1, 3], [2, 3, 1, 4]}$. The optimal encoding of these permutations is

  

• All $2$-similar permutations must allow the intervals $[1, 3]$ and $[2, 4]$ to hold their shapes. Therefore, the set of all $2$-similar permutations is ${[3, 4, 1, 2], [2, 4, 1, 3]}$. The optimal encoding of these permutations is

  

• All $3$-similar permutations must allow the intervals $[1, 3]$, $[2, 4]$, and $[1, 4]$ to hold their shapes. Therefore, the set of all $3$-similar permutations only includes $[2, 4, 1, 3]$. The optimal encoding of this permutation is

  

对于第一个测试用例：

• 所有 $1$-相似排列必须允许区间 $[1, 3]$ 保持其形状。因此，所有 $1$-相似排列的集合为 ${[3, 4, 2, 1], [3, 4, 1, 2], [2, 4, 1, 3], [2, 3, 1, 4]}$。这些排列的最优编码为

  

• 所有 $2$-相似排列必须允许区间 $[1, 3]$ 和 $[2, 4]$ 均保持其形状。因此，所有 $2$-相似排列的集合为 ${[3, 4, 1, 2], [2, 4, 1, 3]}$。这些排列的最优编码为

  

• 所有 $3$-相似排列必须允许区间 $[1, 3]$、$[2, 4]$ 和 $[1, 4]$ 均保持其形状。因此，所有 $3$-相似排列的集合仅包含 $[2, 4, 1, 3]$。该排列的最优编码为