CF1485E.Move and Swap

普及/提高-

通过率：0%

AC君温馨提醒

该题目为【codeforces】题库的题目，您提交的代码将被提交至codeforces进行远程评测，并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供，我们无法保证该服务的稳定性，若提交后无反应，请等待一段时间后再进行重试。

题目描述

You are given $n - 1$ integers $a_2, \dots, a_n$ and a tree with $n$ vertices rooted at vertex $1$ . The leaves are all at the same distance $d$ from the root.

Recall that a tree is a connected undirected graph without cycles. The distance between two vertices is the number of edges on the simple path between them. All non-root vertices with degree $1$ are leaves. If vertices $s$ and $f$ are connected by an edge and the distance of $f$ from the root is greater than the distance of $s$ from the root, then $f$ is called a child of $s$ .

Initially, there are a red coin and a blue coin on the vertex $1$ . Let $r$ be the vertex where the red coin is and let $b$ be the vertex where the blue coin is. You should make $d$ moves. A move consists of three steps:

Move the red coin to any child of $r$ .
Move the blue coin to any vertex $b'$ such that $dist(1, b') = dist(1, b) + 1$ . Here $dist(x, y)$ indicates the length of the simple path between $x$ and $y$ . Note that $b$ and $b'$ are not necessarily connected by an edge.
You can optionally swap the two coins (or skip this step).

Note that $r$ and $b$ can be equal at any time, and there is no number written on the root.

After each move, you gain $|a_r - a_b|$ points. What's the maximum number of points you can gain after $d$ moves?

输入格式

The first line contains a single integer $t$ ( $1 \le t \le 10^4$ ) — the number of test cases.

The first line of each test case contains a single integer $n$ ( $2 \leq n \leq 2 \cdot 10^5$ ) — the number of vertices in the tree.

The second line of each test case contains $n-1$ integers $v_2, v_3, \dots, v_n$ ( $1 \leq v_i \leq n$ , $v_i \neq i$ ) — the $i$ -th of them indicates that there is an edge between vertices $i$ and $v_i$ . It is guaranteed, that these edges form a tree.

The third line of each test case contains $n-1$ integers $a_2, \dots, a_n$ ( $1 \leq a_i \leq 10^9$ ) — the numbers written on the vertices.

It is guaranteed that the sum of $n$ for all test cases does not exceed $2 \cdot 10^5$ .

输出格式

For each test case, print a single integer: the maximum number of points you can gain after $d$ moves.

输入输出样例

输入#1

4
14
1 1 1 2 3 4 4 5 5 6 7 8 8
2 3 7 7 6 9 5 9 7 3 6 6 5
6
1 2 2 3 4
32 78 69 5 41
15
1 15 1 10 4 9 11 2 4 1 8 6 10 11
62 13 12 43 39 65 42 86 25 38 19 19 43 62
15
11 2 7 6 9 8 10 1 1 1 5 3 15 2
50 19 30 35 9 45 13 24 8 44 16 26 10 40

输出#1

说明/提示

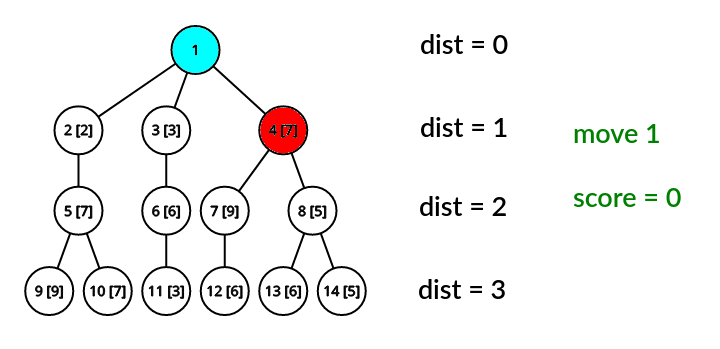
In the first test case, an optimal solution is to:

move $1$ : $r = 4$ , $b = 2$ ; no swap;
move $2$ : $r = 7$ , $b = 6$ ; swap (after it $r = 6$ , $b = 7$ );
move $3$ : $r = 11$ , $b = 9$ ; no swap.

The total number of points is $|7 - 2| + |6 - 9| + |3 - 9| = 14$ .

In the second test case, an optimal solution is to:

move $1$ : $r = 2$ , $b = 2$ ; no swap;
move $2$ : $r = 3$ , $b = 4$ ; no swap;
move $3$ : $r = 5$ , $b = 6$ ; no swap.

The total number of points is $|32 - 32| + |78 - 69| + |5 - 41| = 45$ .

首页