CF643B.Bear and Two Paths

Bearland has n cities, numbered 1 through n. Cities are connected via bidirectional roads. Each road connects two distinct cities. No two roads connect the same pair of cities.

Bear Limak was once in a city a and he wanted to go to a city b. There was no direct connection so he decided to take a long walk, visiting each city exactly once. Formally:

• There is no road between a and b.
• There exists a sequence (path) of n distinct cities _v_1, _v_2, ..., v__n that _v_1 = a, v__n = b and there is a road between v__i and v__i + 1 for .

On the other day, the similar thing happened. Limak wanted to travel between a city c and a city d. There is no road between them but there exists a sequence of n distinct cities _u_1, _u_2, ..., u__n that _u_1 = c, u__n = d and there is a road between u__i and u__i + 1 for .

Also, Limak thinks that there are at most k roads in Bearland. He wonders whether he remembers everything correctly.

Given n, k and four distinct cities a, b, c, d, can you find possible paths (_v_1, ..., v__n) and (_u_1, ..., u__n) to satisfy all the given conditions? Find any solution or print -1 if it's impossible.

Bearland 有 $n$ 座城市，编号为 $1$ 到 $n$。城市之间通过双向道路相连。每条道路连接两个不同的城市，且任意两座城市之间至多只有一条道路。

熊 Limak 曾身处城市 $a$，希望前往城市 $b$。由于 $a$ 与 $b$ 之间没有直接道路，他决定进行一次长距离步行，恰好访问每座城市一次。形式化地：

• $a$ 与 $b$ 之间没有道路；
• 存在一个由 $n$ 个互不相同的城市的序列（路径）$v_1,\,v_2,\,\dots,\,v_n$，满足 $v_1 = a$，$v_n = b$，且对每个 $i = 1, 2, \dots, n-1$，$v_i$ 与 $v_{i+1}$ 之间存在一条道路。

另一天，类似的事情再次发生：Limak 想在城市 $c$ 与城市 $d$ 之间通行。$c$ 与 $d$ 之间也没有道路，但存在一个由 $n$ 个互不相同的城市的序列 $u_1,\,u_2,\,\dots,\,u_n$，满足 $u_1 = c$，$u_n = d$，且对每个 $i = 1, 2, \dots, n-1$，$u_i$ 与 $u_{i+1}$ 之间存在一条道路。

此外，Limak 认为 Bearland 中至多有 $k$ 条道路。他怀疑自己是否记错了所有细节。

给定 $n$、$k$ 以及四个互不相同的城市 $a$、$b$、$c$、$d$，你能否构造出满足上述所有条件的两条路径 $(v_1,\dots,v_n)$ 和 $(u_1,\dots,u_n)$？若存在解，请输出任意一组；否则输出 $-1$。

The first line of the input contains two integers n and k (4 ≤ n ≤ 1000, n - 1 ≤ k ≤ 2_n_ - 2) — the number of cities and the maximum allowed number of roads, respectively.

The second line contains four distinct integers a, b, c and d (1 ≤ a, b, c, d ≤ n).

输入的第一行包含两个整数 $n$ 和 $k$（$4 ≤ n ≤ 1000$，$n - 1 ≤ k ≤ 2n - 2$），分别表示城市的数量和允许修建的最大道路数量。

第二行包含四个互不相同的整数 $a$、$b$、$c$ 和 $d$（$1 ≤ a, b, c, d ≤ n$）。

Print -1 if it's impossible to satisfy all the given conditions. Otherwise, print two lines with paths descriptions. The first of these two lines should contain n distinct integers _v_1, _v_2, ..., v__n where _v_1 = a and v__n = b. The second line should contain n distinct integers _u_1, _u_2, ..., u__n where _u_1 = c and u__n = d.

Two paths generate at most 2_n_ - 2 roads: (_v_1, _v_2), (_v_2, _v_3), ..., (v__n - 1, v__n), (_u_1, _u_2), (_u_2, _u_3), ..., (u__n - 1, u__n). Your answer will be considered wrong if contains more than k distinct roads or any other condition breaks. Note that (x, y) and (y, x) are the same road.

如果无法满足所有给定条件，则输出 -1。否则，输出两行路径描述：
第一行包含 $n$ 个互不相同的整数 $v_1,\,v_2,\,\dots,\,v_n$，其中 $v_1 = a$ 且 $v_n = b$；
第二行包含 $n$ 个互不相同的整数 $u_1,\,u_2,\,\dots,\,u_n$，其中 $u_1 = c$ 且 $u_n = d$。

这两条路径至多生成 $2n - 2$ 条道路：$(v_1,\,v_2),\,(v_2,\,v_3),\,\dots,\,(v_{n-1},\,v_n),\,(u_1,\,u_2),\,(u_2,\,u_3),\,\dots,\,(u_{n-1},\,u_n)$。若你的答案中包含超过 $k$ 条互不相同的道路，或违反任何其他条件，则视为错误。注意，$(x,\,y)$ 与 $(y,\,x)$ 表示同一条道路。

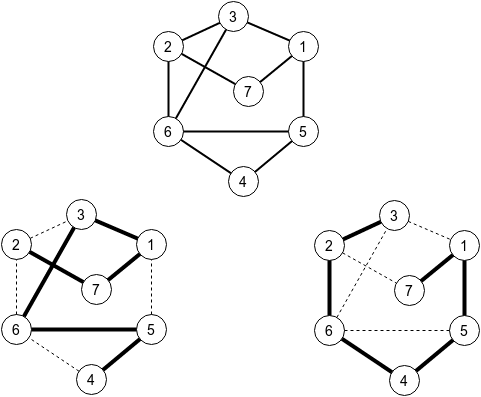
In the first sample test, there should be 7 cities and at most 11 roads. The provided sample solution generates 10 roads, as in the drawing. You can also see a simple path of length n between 2 and 4, and a path between 7 and 3.

在第一个样例测试中，应有 7 座城市，且最多有 11 条道路。所提供的样例解生成了 10 条道路，如图所示。你还可以看到一条长度为 $n$ 的简单路径连接城市 2 和城市 4，以及一条连接城市 7 和城市 3 的路径。